这道题是原本 AK 杯网络赛的压轴题。本题的两个难点如下：

1. 求出跑到离该签到点恰为 100m 的位置坐标
2. 判断从一个点前往另一个签到点外的路线上可能会顺便完成其他的签到任务分别是哪些

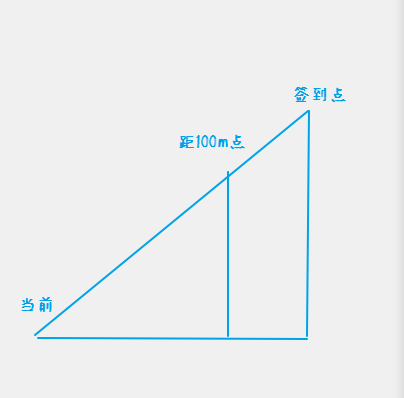
对第一个问题，为避免斜率不存在的特判，可以使用向量分解的思维，分别直接计算横纵坐标。当前点、恰为 100m 的点、通过坐标轴平行作辅助点能组成一个三角形，当前点、签到点、通过坐标轴平行作辅助点能组成另一个三角形。然后分别跟坐标轴平行边与斜边作比例就可以求出横纵坐标了。

对第二个问题，可以转化为对于每个签到点，距一条由两端点(当前点、距 100m 点)确定的线段的距离是否小于等于 100m 。该问题可以用计算几何模板求出，用向量算法。抽象为求 C 点距线段 AB 的距离，可以参考 这篇文章 ，篇幅较长，这里不赘述。

其他部分代码的难度不高，具体实现细节可参考下面代码：

C++

#include <bits/stdc++.h>
#pragma GCC optimize(2)
using namespace std;
typedef long long ll;
typedef double db;
#define sc(x) scanf("%lld", &x)
#define il inline
#define big 1e18
ll t, p[6], vis[6];
db ans, x[6], y[6], rad = 100, misat = 2500;
//两点距离
db d(db ax, db ay, db bx, db by)
{
    return sqrt((ax - bx) * (ax - bx) + (ay - by) * (ay - by));
}
//两向量外积
db cross(db ax, db ay, db bx, db by)
{
    return ax * by - ay * bx;
}
//两向量内积
db dot(db ax, db ay, db bx, db by)
{
    return ax * bx + ay * by;
}
//点到线段的距离 d_point_segment
db dps(db px, db py, db ax, db ay, db bx, db by)
{
    if (dot(bx - ax, by - ay, px - ax, py - ay) < 0.0)
        return d(px, py, ax, ay);
    if (dot(ax - bx, ay - by, px - bx, py - by) < 0.0)
        return d(px, py, bx, by);
    return abs(cross(ax - px, ay - py, bx - px, by - py) / d(ax, ay, bx, by));
}
signed main()
{
    sc(t);
    while (t--)
    {
        ans = big;
        for (ll i = 0; i <= 4; ++i)
        {
            scanf("%lf%lf", &x[i], &y[i]);
            p[i] = i;
        }
        do
        {
            db dis = 0, ax = x[0], ay = y[0], bx, by, di, cx, cy;
            memset(vis, 0, sizeof vis);
            for (ll i = 1; i <= 4; ++i)
            {
                if (d(ax, ay, x[i], y[i]) <= rad)
                {
                    vis[i] = true;
                }
            }
            for (ll i = 1; i <= 4; ++i)
            {
                if (vis[p[i]])
                {
                    continue;
                }
                bx = x[p[i]], by = y[p[i]];
                di = d(ax, ay, bx, by);
                dis += di - rad;
                cx = ax + (di - rad) / di * (bx - ax);
                cy = ay + (di - rad) / di * (by - ay);
                vis[p[i]] = true;
                for (ll j = 1; j <= 4; ++j)
                {
                    if (!vis[j] && dps(x[j], y[j], ax, ay, cx, cy) < rad)
                    {
                        vis[j] = true;
                    }
                }
                ax = cx, ay = cy;
            }

            if (dis >= misat)
            {
                ans = min(ans, dis);
            }
        } while (next_permutation(p + 1, p + 5));
        if (ans == big)
        {
            printf("no\n");
        }
        else
        {
            printf("%.0lf\n", ans);
        }
    }
    return 0;
}

Python

from math import *
dfn = [0, 0, 0, 0]
vis = [0, 0, 0, 0]
p = []


def dfs(h):
    if h == 4:
        p.append(dfn[:])
    else:
        for i in range(4):
            if not vis[i]:
                vis[i] = 1
                dfn[h] = i
                dfs(h+1)
                vis[i] = 0


dfs(0)


def dis(x1, y1, x2, y2):
    return ((x1-x2)**2+(y1-y2)**2)**0.5


def walk(x1, y1, x2, y2):
    s = dis(x1, y1, x2, y2)
    k = (s-100)/s
    x3 = x1+k*(x2-x1)
    y3 = y1+k*(y2-y1)
    return [x3, y3, s-100]


def dot(x1, y1, x2, y2):
    return x1*x2+y1*y2


def cross(x1, y1, x2, y2):
    return x1*y2-x2*y1


def pdis(x1, y1, x2, y2, x3, y3):
    if(dot(x2-x1, y2-y1, x3-x1, y3-y1) < 0.0):
        return dis(x1, y1, x3, y3)
    if(dot(x1-x2, y1-y2, x3-x2, y3-y2) < 0.0):
        return dis(x2, y2, x3, y3)
    return abs(cross(x2-x1, y2-y1, x3-x1, y3-y1)/dis(x1, y1, x2, y2))


for t in range(int(input())):
    x0, y0 = [int(i) for i in input().strip().split()]
    x = []
    y = []
    for i in range(4):
        x1, y1 = [int(i) for i in input().strip().split()]
        x.append(x1)
        y.append(y1)
    ans = 1e18
    for h in range(24):
        d = 0
        xn = x0
        yn = y0
        vi = []
        for i in range(4):
            vi.append(dis(xn, yn, x[p[h][i]], y[p[h][i]]) <= 100)
        for i in range(4):
            if vi[i]:
                continue
            x1 = x[p[h][i]]
            y1 = y[p[h][i]]
            wr = walk(xn, yn, x1, y1)
            d += wr[2]
            vi[i] = True
            for j in range(4):
                if not vi[j] and pdis(wr[0], wr[1], xn, yn, x[p[h][j]], y[p[h][j]]) <= 100:
                    vi[j] = True
            xn = wr[0]
            yn = wr[1]
        if d >= 2500:
            ans = min(ans, d)

    if ans == 1e18:
        print('no')
    else:
        print(round(ans))