冯·诺依曼：微积分是现代数学的第一个成就，而且怎样评价它的重要性都不为过。我认为，微积分比其他任何事物都更清楚地表明了现代数学的发端；而且，作为其逻辑发展的数学分析体系仍然构成了精密思维中最伟大的技术进展。

微积分学的创立，极大地推动了数学的发展，过去很多用初等数学无法解决的问题，运用微积分，这些问题往往迎刃而解，显示出微积分学的非凡威力。

微积分的发展历史表明了人的认识是从生动的直观开始，进而达到抽象思维，也就是从感性认识到理性认识的过程。人类对客观世界的规律性的认识具有相对性，受到时代的局限。随着人类认识的深入，认识将一步一步地由低级到高级、由不全面到比较全面地发展。人类对自然的探索永远不会有终点。
微积分的一个基本应用，是求平面直角坐标内一条函数曲线 y=f(x) 在给定的区间内 x∈[a,b] 与自变量轴线 x 所围成的面积。在常见的几何图形内，圆形是一个很好的例子。

那么怎么运用微积分来求圆的面积呢？过程很简单：把圆形切割成一条条的线，只要这些线的长度能用函数的形式写出来，就能将圆的面积公式推导出来。

基于圆形的轴对称和各向同性，我们有两种切割线的方法，一种是水平切割，一种是同心圆切割。

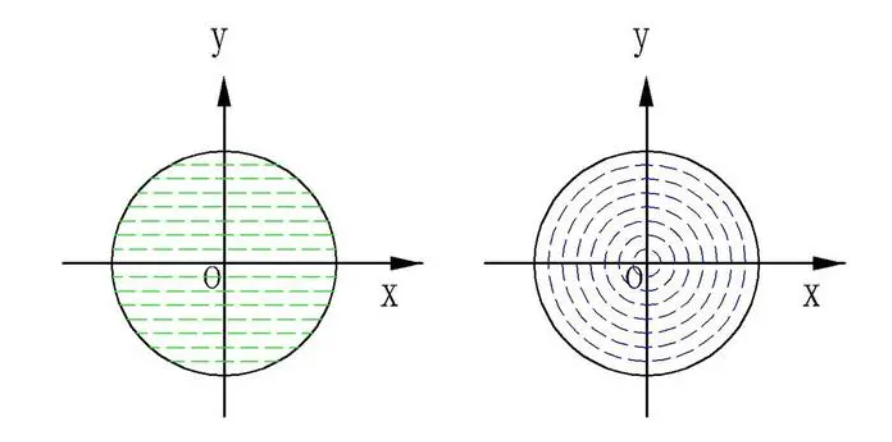
微积分的原理是导函数和原函数的相互转换，也是微分过程和积分过程的互逆。其中，导数 f'(x) 负责描述构成平面图形的直线的函数，微分 f'(x)*△x 在定义区间上的集合负责描述整个平面图形，积分负责计算。

在这里，用水平切割线求圆形面积，需要先用函数来表达水平切割线的长度。

如上图，在区间 x∈[0,R] 上，任意取值 x，对应的有 x^2+y^2=R^2，于是在第一象限内有： y=\sqrt{R^2-x^2} 由圆的对称性，我们只需计算第一象限内的四分之一圆的面积即可。于是，得圆形面积的积分表达式： S=4\int_{0}^{R}{\sqrt{R^2-x^2}}dx 以 f(x)=\sqrt{R^2-x^2} 为导函数，通过查不定积分表，得到它的原函数:

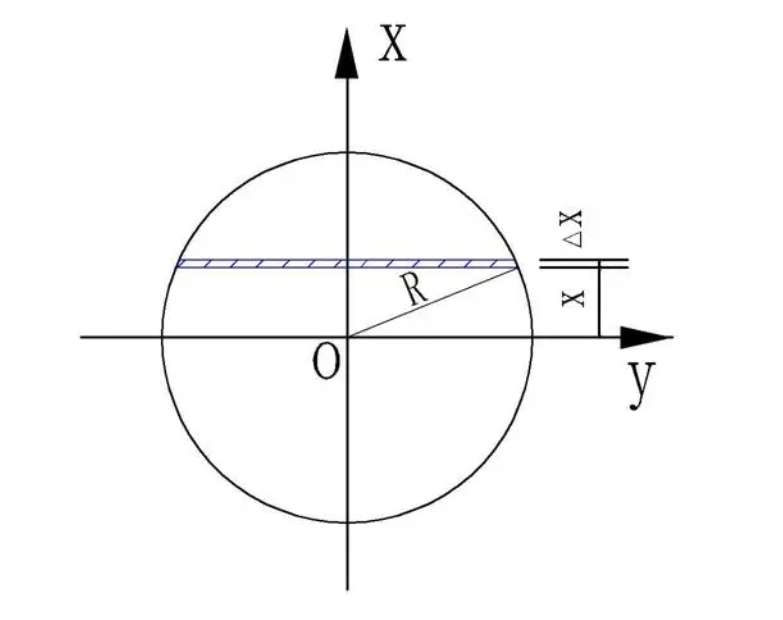
F(x)=\frac{x}{2}\sqrt{R^2-x^2}+\frac{R^2}{2}arcsin{\frac{x}{2}}+C ​

然后，计算圆形的面积:

\begin{cases} S&=4\int_{0}^{R}{\sqrt{R^2-x^2}}dx\\\ \quad \\ &=4(\frac{x}{2}\sqrt{R^2-x^2}+\frac{R^2}{2}arcsin\frac{x}{R})|_{0}^{R}\\\ \quad \\ &=4[(\frac{R}{2}\sqrt{R^2-R^2}+\frac{R^2}{2}arcsin{\frac{R}{R}})-(\frac{0}{2}\sqrt{R^2-0^2}+\frac{R^2}{2}arcsin{\frac{0}{R}})]\\\ \quad \\ &=4\frac{R^2}{2}\cdot\frac{π}{2} \\\ \quad \\ &=πR^2 \end{cases}

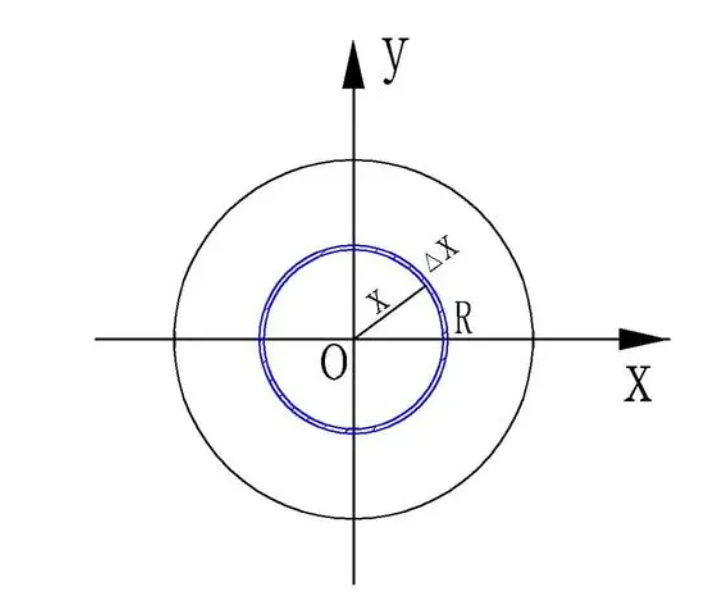
亦或者使用割圆法：

基于圆形的各向共性，按同心圆切割可以使计算简单一些。

按同心圆的方式切割，导函数就是圆形的周长公式，于是，得圆形面积的积分表达式： S=\int_{0}^{R}2πxdx 然后，计算圆形的面积： S=\int_{0}^{R}2πxdx=πx^2|_{0}^{R}=πR^2 第二种方法虽然简单一些，但是割圆法是极限运算的方法，只适用于圆形这种特殊的图形，对于一般可积的图形就用不上了，不具有一般性，常规的做法还是用第一种。

怎么样，现在的你，是不是学到了许多知识？有没有对微积分产生浓厚兴趣？请你输出"xue fei le"，表示你已经学会(fei)了微积分。

无输入数据

输出一行 xue fei le

xue fei le