1975. 收费站
你们计算完后发现,幻想乡的基建甚至有高速公路,但是收费贵贵(Powered by 灵梦)。然而,高速公路尚未设立收费站,只有设立收费站后才能通行并调配食材。管理员幽幽子想把这个重要的任务交给你,如果耽误了幽幽子炫饭就会被幽幽子做成麻薯吃掉 (穿越三人集体波奇酱附体)。
有 n 个地区,编号从 1 开始。有 m 条单向通行的道路。道路 u\to v 表示只能从地区 u 通向地区 v。定义从地区 x 通往地区 y 的路径是若干条不重道路的有序序列,满足首条道路起点为 x,最后一条道路终点为 y,其他道路的起点都是上一条道路的终点。例如若存在道路 1\to3,3\to2,2\to4 则 1\to 3\to2\to4 是地区 1 到地区 4 的一条路径。
现在一些道路上设置了收费站,使得对每条从地区 1 通往地区 n 的路径,路径上都存在且仅存在一条道路设置了收费站。且希望设置尽可能少的收费站达成上述目标。问至少需要设置多少个收费站,分别设置在哪些道路上。
输入
输入一行两个整数 n,m(2\le n\le10^5,1\le m\le10^5)。
接下来输入 m 行,每行两个整数 u,v(1\le u,v\le n,u\neq v) 代表一条道路 u\to v。保证没有重边,不会成环,且存在至少一条从地区 1 通往地区 n 的路径,且保证对所有 1 < x < n,地区 x 至少有一条路径为 u\to x 和一条路径 x\to v。
输出
输出一行一个整数,代表最小收费站个数 k。
接下来输入 k 行,每行两个整数 u,v(1\le u,v\le n),代表在道路 u\to v 设置收费站。你可以用任意顺序输出道路。
如果有多个设置收费站的方案,你只需要输出任意一个即可。
样例
| 标准输入 复制文本 |
9 9 1 2 2 3 2 4 3 5 4 6 5 7 6 7 7 8 8 9 |
| 标准输出 复制文本 |
1 1 2 |
| 标准输入 复制文本 |
10 12 1 2 1 3 1 4 2 5 3 5 4 6 5 7 6 8 6 9 7 10 8 10 9 10 |
| 标准输出 复制文本 |
2 5 7 1 4 |
| 标准输入 复制文本 |
2 1 1 2 |
| 标准输出 复制文本 |
1 1 2 |
提示
对样例一,道路如图所示:
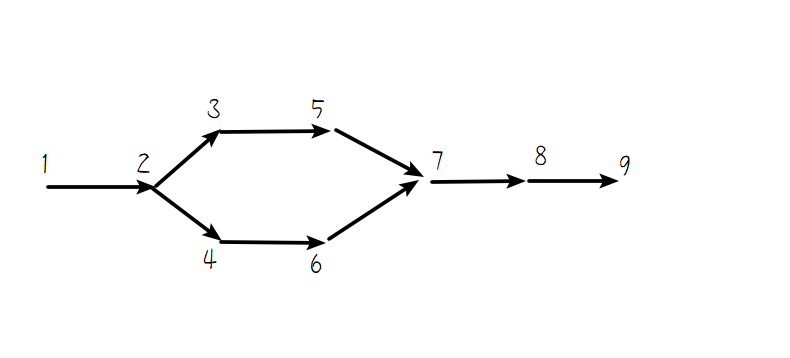
仅有两条 1 到 9 的路径即 1\to2\to3\to5\to7\to8\to9,1\to2\to4\to6\to7\to8\to9。因此,在 1\to 2,7\to 8,8\to 9 三道路的其中一条设置收费站,均能满足目的。
对样例二,道路如图所示:
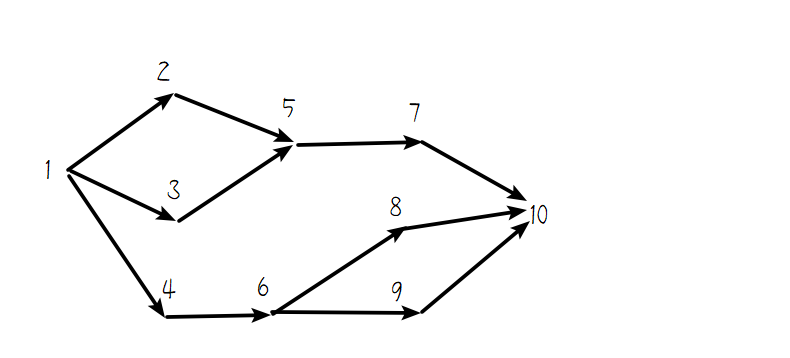
有四条 1 到 10 的道路。要设置最少的收费站,其中一个必须在 5\to7,7\to 10 里选择,另一个在 1\to4,4\to 6 里选择,共四种可行设置方案。
对样例三,道路如图所示:

唯一方案是在 1\to 2 这条唯一道路设置收费站。
来源
2023 SCNUCPC 重现赛