2053. 求分拆数(15分)
曾在上次AK杯之时,Serein便发现了五边形数的具体定义,但 Serein并不满足于此,从中进行深究,发现了可以根据五边形数定理快速计算分拆数。
将正整数 n 分解为若干个正整数之和,称为分拆。设 p_n 代表正整数 n 有多少种不同的分拆方案。例如 p_0=p_1=1,p_2=2,p_3=3,p_4=5,因为 1=1;2=1+1=2;3=1+1+1=1+2=3;4=1+1+1+1=1+1+2=1+3=2+2=4。
将无限多个点按照下图方式摆放,形成无限多个正五边形(下图仅展示四个):
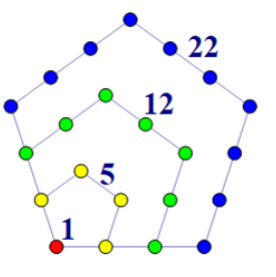
定义第 i 个五边形数是图中第 i 小的五边形边上和内部所包含的点数(特别规定最小的五边形是一个点)。例如,图中,前四个五边形数分别是 1,5,12,22。以第三个五边形为例,它包含的点是红色、黄色和绿色的点,统计得共 12 个。
已知五边形数为 b=1,5,12,22\cdots,定义广义五边形数为 a=1,2,5,7,12,15,22,26,\cdots。即第 2i-1 个广义五边形数为第 i 个五边形数,且第 2i 个广义五边形数总是比第 2i-1 个广义五边形数多 i。根据五边形数定理,可以用如下公式快速计算分拆数: p_i=\sum_{j=1}^{a_j\le i}(-1)^{\lfloor\frac{j+1}{2}\rfloor+1}p_{i-a_{j}}
特别地, p_0=1。其中 \lfloor x\rfloor 为 x 的下取整。即 p_n=p_{n-1}+p_{n-2}-p_{n-5}-p_{n-7}+\cdots。例如 p_2=p_1+p_0=2,p_3=p_2+p_1=3,p_5=p_4+p_3-p_0=3+5-1=7,p_6=p_5+p_4-p_1=5+7-1=11,p_7=p_6+p_5-p_2-p_0=11+7-2-1=15。
给定 n,请你计算并输出 p_n。
输入
输入一行一个整数 n(0\le n\le100)。
输出
输出一行一个整数,代表 p_n。保证给定范围内计算过程不会超出 C/C++ int 所能表示的范围。
样例
| 标准输入 复制文本 |
0 |
| 标准输出 复制文本 |
1 |
| 标准输入 复制文本 |
4 |
| 标准输出 复制文本 |
5 |
| 标准输入 复制文本 |
66 |
| 标准输出 复制文本 |
2323520 |
来源
2023 天梯赛选拔赛 (重现)