注意到起始长度是 $5$ ，之后每次 $n$ 增加 $1$ ，两边各增大 $2$ ，所以总长度为 $5+4n$ ，因此数组每个维度范围不应该小于 $5+4\times30$ ，且一开始可以直接先铺满这个区域全部是 . ，之后每次画用 $ 替代 . 即可。

使用递归来做的话， 可以设当前区域左上角下标为 $(x,y)$ ，横坐标从上往下，从坐标从左往右。观察可知，除了最中心的小十字之外，其他每一层的大十字都很有规律 (其实中间的十字也可以用相同的规律生成)。假设先不考虑中心小十字：

$n \ge 1$ 时，当前区域跨度是 $5+4n$ ，可以以 $(x,y)$ 为左上角，画长为 $1+4n$ 的四条直线和四个内折的角（转化为八条直线）。设 $l=4n$

则这么一个大十字可具体为：

1. 端点在 $(x+2,y),(x+2+l,y)$ 的直线
2. 端点在 $(x,y+2),(x,y+2+l)$ 的直线
3. 端点在 $(x+2,y+4+l),(x+2+l,y+4+l)$ 的直线
4. 端点在 $(x+4+l,y+2),(x+4+l,y+2+l)$ 的直线
5. 端点在 $(x+2,y),(x+2,y+2)$ 的直线
6. 端点在 $(x,y+2),(x+2,y+2)$ 的直线
7. 端点在 $(x,y+2+l),(x+2,y+2+l)$ 的直线
8. 端点在 $(x+2,y+2+l),(x+2,y+4+l)$ 的直线
9. 端点在 $(x+2+l,y),(x+2+l,y+2)$ 的直线
10. 端点在 $(x+2+l,y+2),(x+4+l,y+2)$ 的直线
11. 端点在 $(x+2+l,y+2+l),(x+4+l,y+2+l)$ 的直线
12. 端点在 $(x+2+l,y+2+l),(x+2+l,y+4+l)$ 的直线

如图所示：

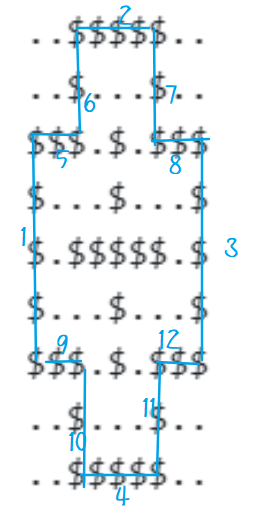
可以设一个绘制直线的函数，然后每次画第 $i$ 个大十字复用 $12$ 次，以减轻工作量。

那么，设 $f(n)$ 是绘制第 $n$ 个大十字，有： $f(n)=f(n-1)+十二条直线$ 特别地，根据上面的十二条直线，我们发现若 $n=0,l=1$ ，恰能对应最中心的小十字。由此，可得 $f$ 定义域为 $n\ge 0$ 。

绘制直线函数可以抽象为画矩形函数(长或宽为 $1$) ，从而避免横竖的分类讨论。

绘制直线和递归函数的具体实现参见代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
char a[131][131];
void line(ll ax, ll ay, ll bx, ll by)
{
    for (ll i = ax; i <= bx; ++i)
    {
        for (ll j = ay; j <= by; ++j)
        {
            a[i][j] = '$';
        }
    }
}
void draw(ll x, ll y, ll l, ll n)
{
    if (n < 0)
    {
        return;
    }
    line(x + 2, y, x + 2 + l, y);
    line(x, y + 2, x, y + 2 + l);
    line(x + 2, y + 4 + l, x + 2 + l, y + 4 + l);
    line(x + 4 + l, y + 2, x + 4 + l, y + 2 + l);
    line(x + 2, y, x + 2, y + 2);
    line(x, y + 2, x + 2, y + 2);
    line(x, y + 2 + l, x + 2, y + 2 + l);
    line(x + 2, y + 2 + l, x + 2, y + 4 + l);
    line(x + 2 + l, y, x + 2 + l, y + 2);
    line(x + 2 + l, y + 2, x + 4 + l, y + 2);
    line(x + 2 + l, y + 2 + l, x + 4 + l, y + 2 + l);
    line(x + 2 + l, y + 2 + l, x + 2 + l, y + 4 + l);
    draw(x + 2, y + 2, l - 4, n - 1);
}
ll n, l;
signed main()
{
    cin >> n;
    l = 5 + 4 * n;
    for (ll i = 0; i < l; ++i)
    {
        for (ll j = 0; j < l; ++j)
        {
            a[i][j] = '.';
        }
    }
    draw(0, 0, 4 * n, n);
    for (ll i = 0; i < l; ++i)
    {
        puts(a[i]);
    }
    return 0;
}