2299. Day11 D - Not Scanning Line
在直角坐标系上,给定 n 个矩形。
对所有的 k=1\sim n,求出平面上被恰好 k 个矩形覆盖的区域的面积。
语法教学
有一些题目的数据值域太大,数的个数量级却小很多,我们可以使用 离散化 来简化。
比如我有一个数组:[5,1007,1145141919810,-20,1007,998244353]
那么根据这些数的相对大小,我们可以把他们映射成:[2,3,5,1,3,4]
具体过程是这样的:
- 我们把原本的数组排序:
[-20,5,1007,1007,998244353,1145141919810]; 然后再将其中重复的元素去掉:
[-20,5,1007,998244353,1145141919810/*,1007*/];再把这些值映射到新的下标:
[1,2,3,4,5]
我们可以将整个数组排序,检查相邻元素是否相同以去重,再通过二分(你已经学会 lower_bound 了!)或者 map(day13内容)来实现此过程。
离散化过程 复杂 而 繁琐 写得头晕?
介绍:unique!
unique(begin,end); // 会将单调递增的数组去重,并返回指向 去重完部分的结尾 的迭代器。
以下演示 0-index int[] 的离散化操作以及离散化映射函数:
int a[10001],ed;
int id(long long x)
{
return lower_bound(a,a+ed,x);
}
//...
sort(a,a+n);
ed=unique(a,a+n)-a;
以下演示 0-index vector 的离散化操作 以及 lambda 函数形式的离散化映射函数:
sort(a.begin(),a.end());
a.erase(unique(a.begin(),a.end()),a.end());
auto id=[&](long long x)->int
{
return lower_bound(a.begin(),a.end(),x)-a.begin();
};
输入
数据的第一行为一个正整数 n(1\leq n \leq 3000),表示给定矩形的个数。
随后 n 行,每行给出四个整数 u,l,d,r(-10^9 \leq u \leq d \leq 10^9,\ -10^9 \leq l \leq r \leq 10^9),表示给出矩形的对角格坐标 (u,l) 和 (d,r)。
输出
输出共一行由空格隔开的 n 个整数,表示对于所有的 k=1\sim n,平面上被恰好 k 个矩形覆盖的区域的面积。
样例
| 标准输入 复制文本 |
4 2 1 2 1 2 3 3 4 3 4 5 5 1 2 6 4 |
| 标准输出 复制文本 |
16 5 1 0 |
| 标准输入 复制文本 |
8 7 7 7 7 4 2 7 3 4 1 7 4 5 2 6 3 3 6 8 6 8 8 8 8 4 7 4 7 3 8 3 8 |
| 标准输出 复制文本 |
18 4 4 0 0 0 0 0 |
提示
样例 1 中绘制的矩形如图:
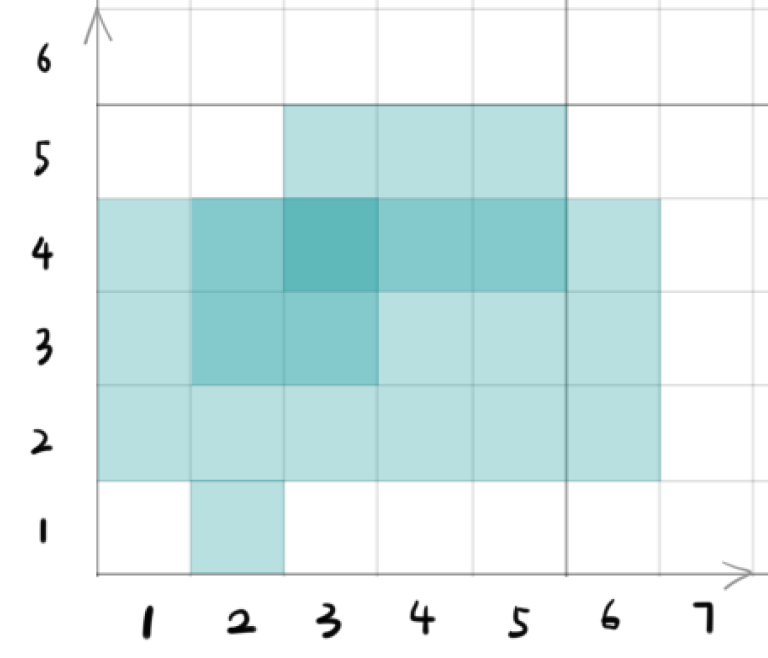
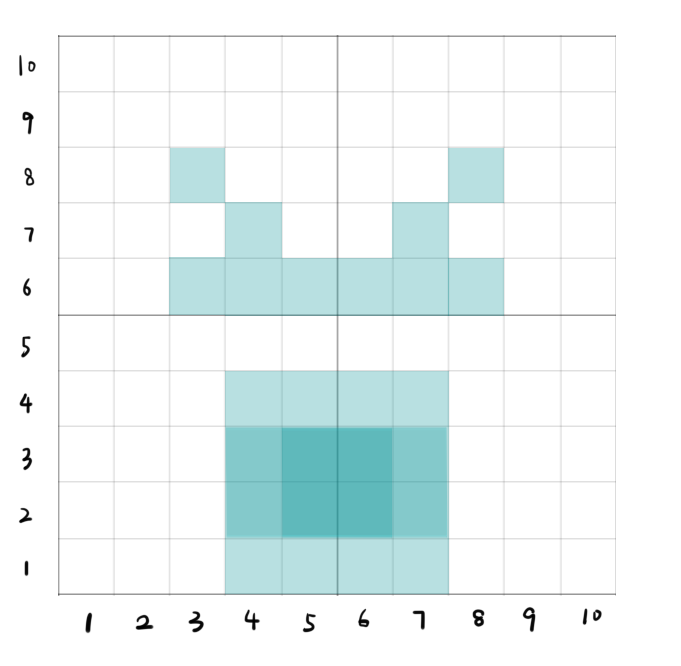
样例 2 中绘制的矩形如图: