题目背景

你知道一颗末影之眼就可以定位确定要塞的大致位置吗?

题目描述

自 15w43a (1.9) 更新后，每个世界会生成 128 个要塞，构成八个要塞环，本文将讨论如何使用一颗末影之眼定位要塞，并请你编写一个定位要塞的程序

128 个要塞中，距离原点最近的三个落于以世界原点为圆心，半径为 1280 ~ 2816 的圆环上，互成 120° 角。在抛出末影之眼时，它会以抛出位置为端点，构成一条指向最近要塞方向的射线。

试证明处在距原点 1280 格范围内的玩家，抛出的末影之眼必定定位到第一环的要塞：

• 1. 模型建立

  1.1 坐标系定义

  建立二维极坐标系：

  • 世界原点 O(0,0) 为圆心

  • 要塞位置 S_i 服从环形分布：

  • 第一环： S_i \in {|S|_2 \in [1280,2816]}

  • 第二环： S_j \in {|S|_2 \in [4352,5888]}

  1.2 末影之眼行为模型

  定义距离函数：D(P,S) = \sqrt{(x_S-x_P)^2 + (z_S-z_P)^2}

  末影之眼遵循最近邻原则：S_{target} = \mathop{\arg\min}\limits_{S \in \mathbb{S}} D(P,S)

• 2. 主要证明

  2.1 引理1（距离下限）

  对于任意 P 满足 |P|_2 \leq 1280 和第二环要塞S_j，有：D(P,S_j) \geq 4352 - 1280 = 3072 证明：由三角不等式 |S_j| - |P| \leq D(P,S_j) 直接可得。

  2.2 引理2（距离上限）

  存在第一环要塞 S_i 使得：D(P,S_i) \leq 2816 + 1280 = 4096 且实际最大值更小：\max D(P,S_i) \approx 2\sqrt{1280 \times 2816} \approx 3797 \quad \text{(通过极值分析)}

  2.3 定理证明

  采用反证法：

  1. 假设存在 S_j 使 D(P,S_j) < D(P,S_i)
  2. 由引理 1 得 D(P,S_j) \geq 3072
  3. 但存在 S_i 使 D(P,S_i) \leq 1280（当 P 与 S_i 同象限时）
  4. 产生矛盾，故假设不成立

• 3. 结论

  在 |P|_2 \leq 1280 范围内，D(P,S_i) < D(P,S_j) 恒成立

  通过 1000 次要塞随机生成测试，并对结果进行三次回归，拟合得到以下经验方程：

  平均传送误差 y = 2E-7x^3 - 6E-4x^2 - 0.0837x + 1727.7

  最佳传送误差 y = 2E-7x^3 - 5E-4x^2 - 0.4192x + 1482.1

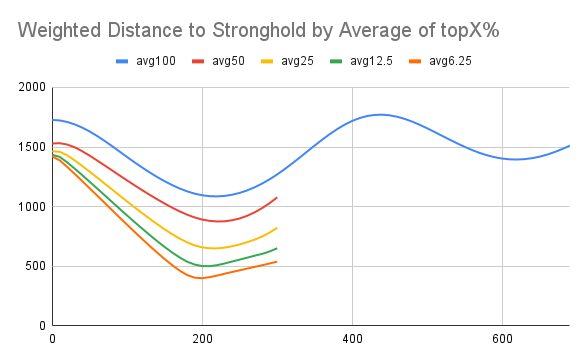
通过经验方程，可以知道，要塞落在以原点为圆心，半径为 1728 格的圆上的可能性最大。在圆内抛出一颗末影之眼，观测其偏移角，可以求得末影之眼射线与圆的交点。

具体地：

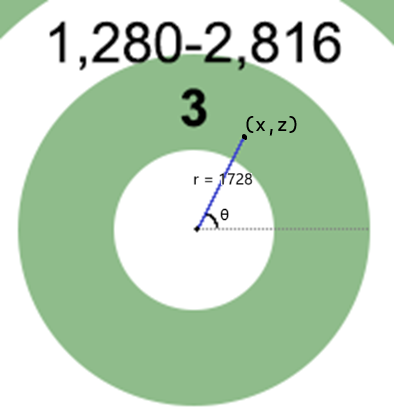
​ 设当前玩家所处坐标为 (x_1,z_1)，末影之眼的射线角为 \theta，建立点斜式方程并于圆的方程联立，得到：

z^2+x^2=1728^2

z-z_1=tan(\theta)(x-x_1)

​ 其中 (x,z) 就是要塞的预测位置。

​ 为简化此模型，我们假设玩家处于世界原点，即 (x_1,z_1) 为 (0,0)； ​ 保证射线指向 x 轴和 z 轴正方向 ，给定射线角 \theta； ​ 试求要塞预测位置 (x,z)

每个测试由多个测试用例组成。第一行包含一个整数 t (1 \leq t \leq 100) - 测试用例数。下面 t 行描述测试用例。

每个测试用例占一行，输入一个整数，表示射线角 \theta (0°\leq\theta\leq90°)

对于每个测试用例，输出一行，两个非负整数，表示预测的要塞位置 (x,z)，你的答案被认为正确，当且仅当输出坐标与方程的精确解的坐标的欧几里得距离严格小于 \sqrt{2}