2156. 变成长方形了
题目背景
让我们来学习一下扫描线
扫描线一般运用在图形上面,它和它的字面意思十分相似,就是一条线在整个图上扫来扫去,它一般被用来解决图形面积,周长,以及二维数点等问题。
比如这个题,需要求 n 个四边平行于坐标轴的矩形的面积并,也就是在二维坐标系上,给出多个矩形的左下以及右上坐标,求出所有矩形构成的图形的面积。
过程
根据图片可知总面积可以直接暴力即可求出面积,如果数据大了怎么办?这时就需要讲到 扫描线 算法。
现在假设我们有一根线,从下往上开始扫描:
如图所示,把整个矩形分成如图各个颜色不同的小矩形,小矩形的高是扫过的距离,然而矩形的水平宽一直在变化。
给每一个矩形的上下边进行标记,下面的边标记为 1,上面的边标记为 -1。每遇到一个水平边时,让这条边(在横轴投影区间)的权值加上这条边的标记。
- 这个操作类似遍历括号序列:开括号加 1,闭括号减 1,「权值」对应当前位置的深度,「权值」是否大于 0,对应当前在不在括号里,也就是这段区间是否记入小矩形的宽度。
小矩形(不一定只有一个)的宽度就是整个数轴上权值大于 0 的区间总长度。
实现
用线段树维护矩形的长,也就是整个数轴上覆盖次数大于 0 的点。需求列举如下:
- 一段区间权值加 1、减 1。
- 统计整个数轴上,区间权值大于 0 的「区间长度和」。
如果你尝试直接用普通线段树模板来实现的话,也许会遇到些挫折。具体地,由于在区间加时,即使修改区间和节点管理区间重合,我们还是不能常数时间知道覆盖次数如何变化。这是因为我们不能直接知道:管理范围里有多长的区间会从 1 变成 0(从 0 变成 1)。
这道题只需要朴素的分治就能实现:维护每个节点管理区间中「整体 修改的权值和 w[]」(类似不用下放的懒惰标记)和「覆盖长度 v[]」两个信息。
还有就是不要忘了离散化
题目内容
如上所说,给你 n 个长方形的端点坐标,求所有被长方形覆盖的位置的总面积
输入
第一行一个正整数 n。(1 \leq n \leq 100)
接下来 n 行每行四个非负整数 x_1, y_1, x_2, y_2,表示一个矩形的左下角坐标为 (x_1, y_1), 右上角坐标为 (x_2, y_2)。
保证 (0 \leq x_1 < x_2 \leq 100), (0 \leq y_1 < y_2 \leq 100)
输出
一行一个正整数,表示 n 个矩形的并集覆盖的总面积。
样例
| 标准输入 复制文本 |
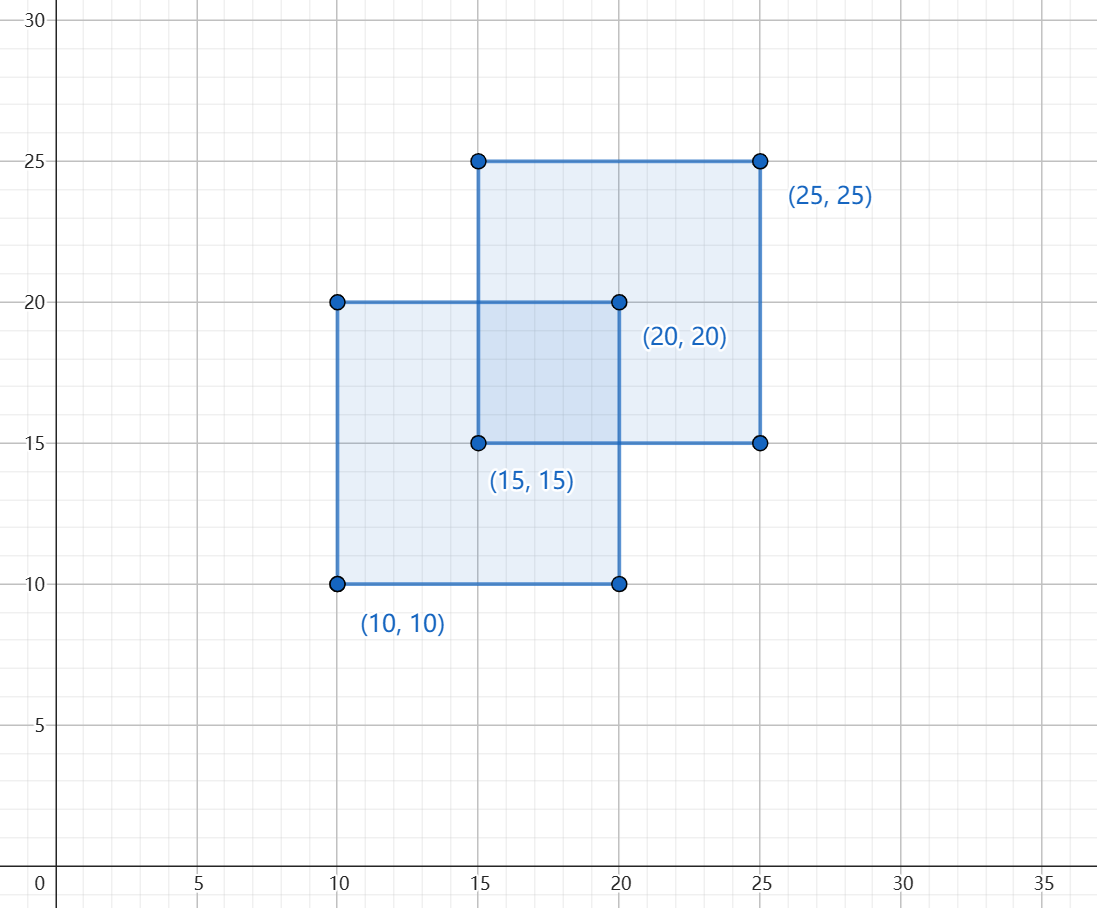
2 10 10 20 20 15 15 25 25 |
| 标准输出 复制文本 |
175 |
提示
对于 100\% 的数据,1 \le n \le 100,(0 \leq x_1 < x_2 \leq 100), (0 \leq y_1 < y_2 \leq 100)
样例一含有两个矩形,面积并是 175, 如下图: