1730. 函数2
给定常数 a,b,c,d,e,l,r ,求下列函数在定义域 [l,r] 的最大值: f(x)=\sin(\dfrac xa)+\sin(\dfrac xb)+\sin(\dfrac xc)+\sin(\dfrac xd)+\sin(\dfrac xe)
输入
输入一行七个整数 a,b,c,d,e,l,r(1\le a,b,c,d,e\le10^3,-10^3\le l< r\le10^3)
输出
输入一行一个实数,代表函数最大值。你的答案被视作是正确的当且仅当与标准答案绝对误差不超过 10^{-2}
样例
| 标准输入 复制文本 |
1 1 1 1 1 0 10 |
| 标准输出 复制文本 |
5 |
| 标准输入 复制文本 |
1 2 3 4 5 0 58 |
| 标准输出 复制文本 |
3.353015 |
| 标准输入 复制文本 |
1 2 3 68 95 -233 233 |
| 标准输出 复制文本 |
4.303793 |
提示
样例 1 :
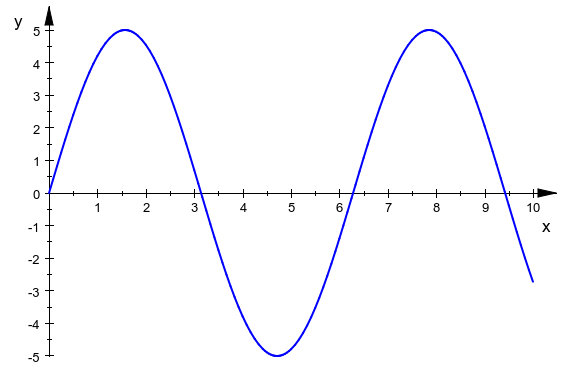
样例 2 :
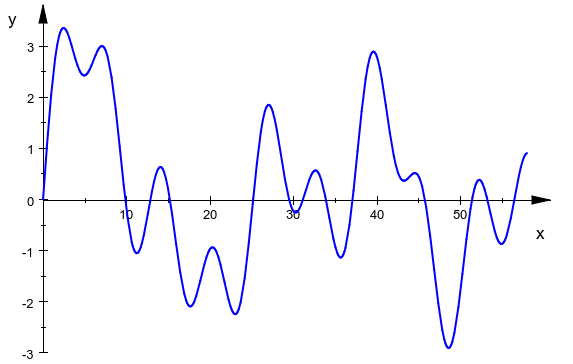
样例 3 :
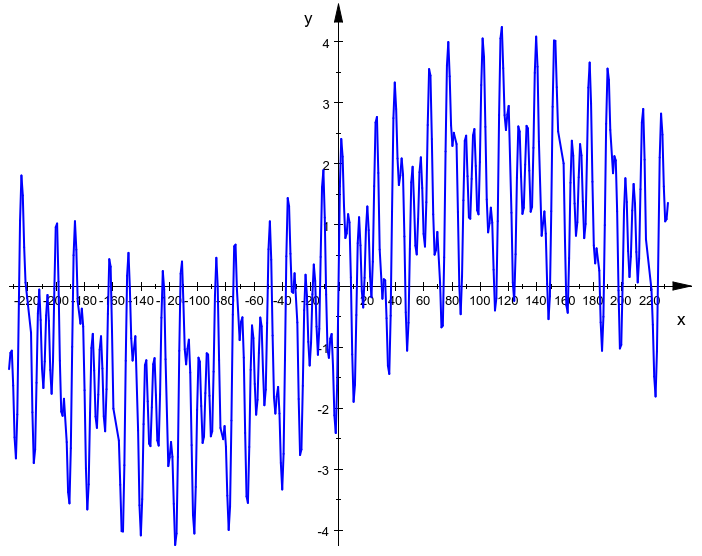
登录以提交代码。