1726. 矩形相交
在平面上给定四个点 A(x_a,y_a),B(x_b,y_b),C(x_c,y_c),D(x_d,y_d),假设矩形一的左下角点为 A,右上角点为 B;矩形一的左下角点为 C,右上角点为 D,判断两个矩形是否相交。
请注意在本题中,两矩形相交当且仅当两个矩形的边框存在公共点。
输入
输入包含多组测试用例。
第一行包含一个整数 t \ (1 \leq t \leq 10^3),表示你需要处理 t 组测试用例。
接下来 t 行每行一组测试用例,包含八个用空格间隔的整数 x_a,y_a,x_b,y_b,x_c,y_c,x_d,y_d \ (-10^9 \leq x_a,y_a,x_b,y_b,x_c,y_c,x_d,y_d \leq 10^9, x_a < x_b, y_a < y_b , x_c < x_d , y_c < y_d),四个点的坐标。
输出
对于每组测试用例,如果两矩形相交,在单独的一行内输出 1,否则输出 0。
样例
| 标准输入 复制文本 |
3 0 0 2 2 1 1 4 6 0 -1 10 11 13 16 58 85 0 0 2 4 1 4 6 6 |
| 标准输出 复制文本 |
1 0 1 |
提示
对于测试用例 1,两个矩形所在位置如下图。
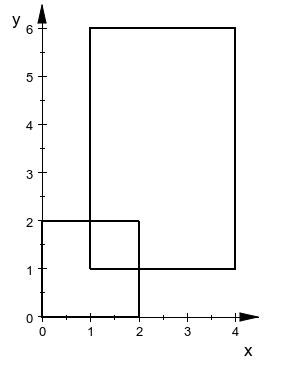
对于测试用例 2,两个矩形所在位置如下图。
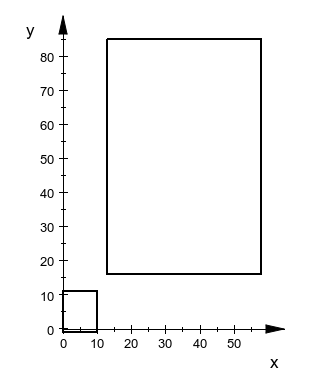
对于测试用例 3,两个矩形所在位置如下图。
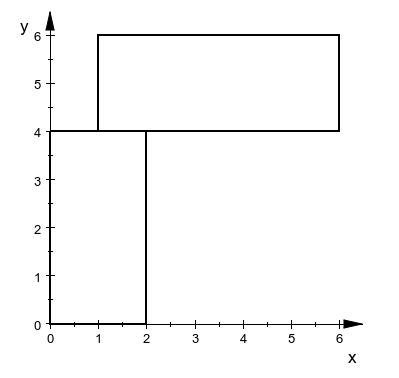
登录以提交代码。