Some birds are not meant to be caged, their feathers are just too bright. jl 很向往空中的飞鸟，于是，sz 找到了鞘翅送给 jl ，让他能够在高空翱翔。

假设天空是一个宽高无限的二维欧几里得平面，y 轴方向从左往右递增，z 轴方向从下往上递增， jl 当前的飞行方向有八个(左上、左、左下、下、右下、右、右上、上)。每秒初会朝着当前方向移动 1 次。方向为上、下、左、右其一时，移动的直线位移是 1 格；否则，移动的直线位移是 \sqrt{1+1}=\sqrt2 格。如图所示：

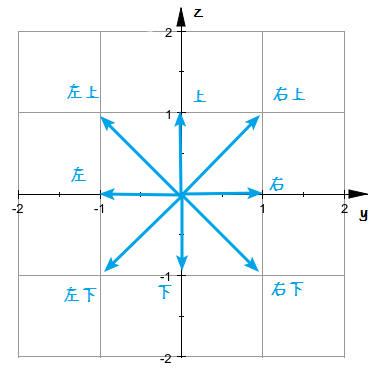
不幸的是，jl 飞行时正处于夜晚。天空中随机生成了若干敌对生物幻翼。定义平面两点 (y_1,z_1),(y_2,z_2) 的距离为 |y_1-y_2|+|z_1-z_2| 。若幻翼当前与 jl 的距离小于等于 64 格，那么在 jl 移动后瞬间，幻翼会在上述八方向中选择一个方向移动，使得移动后在所有的选择里与 jl 的距离最小，可通俗理解为朝着 jl 的坐标跟踪移动。移动位移大小同上。特别地，如果此时幻翼恰好与 jl 在同一格，幻翼不会移动。

• jl 的初始生命值为 20，攻击力恒为 7。 幻翼的初始生命值为 20，攻击力恒为 3。
• jl 可能随时改变飞行方向。若 jl 在某一秒初更改飞行方向，那么从这一秒初开始(包括这一秒)， jl 移动方向会发生变化。
• 方向确定后 jl 和幻翼相继移动（两者的移动方向未必相同），若 jl 与 任意一只幻翼处于同一格，他们会相互攻击一次，攻击伤害值为攻击方的攻击力大小，且不会超过被攻击方的当前生命值，双方生命值的减少量等同于对方的攻击伤害值。
• 假设 jl 与多只幻翼处在同一格，因为鞘翅的玄妙，这一秒内 jl 只受到一次攻击，而多只幻翼将各受到一次 jl 的攻击。这秒的所有攻击结束后，将自动进入下一秒。值得注意的是，幻翼受到攻击之后的 1 秒钟不会移动，而 jl 受到攻击后下一秒仍会继续飞行。
• 若任一方的生命值不为正数，则视为死亡。幻翼死亡后不会继续攻击、移动；若 jl 死亡则会失去宝贵的鞘翅。

约定左上、左、左下、下、右下、右、右上、上 八个方向分别记作 1,2,3,4,5,6,7,8。

记初始时间为第 1 秒初，jl 会飞行 t 秒，在第 t 秒末时，如果 jl 仍存活，他会让 sz 马上用指令将他传送回家，并获得一张一鸣的女装照作为奖励。

输入包含多组测试用例。

第一行包含一个整数 T \ (1 \leq T \leq 10)，表示你需要处理 T 组测试用例。

对于每个测试，首先输入一行一个五个整数 t(1\le t\le10^3),p(0\le p\le t-1),d_0(1\le d_0\le 8)，y_0,z_0(-10^5\le y_0,z_0\le10^5) ，t 代表 jl 飞行的总时长，p 代表 jl 调整飞行方向的次数， d_0 代表 jl 的初始飞行方向。y_0,z_0 代表 jl 的初始坐标。

接下来输入 p 行，每行两个整数 m, d(2\le m\le t, 1\le d\le8)，代表 jl 在第 m 秒初移动前更改的飞行方向为 d。保证 m 严格单调递增。

接下来输入一行一个整数 n(1\le n\le10^3)，代表幻翼的个数。

接下来输入 n 行，每行两个整数 y,z(-10^5\le y,z\le10^5)，代表一个幻翼的初始坐标。

对于每个测试，如果 jl 没能活过 t 秒，在一行内输出lose，并输出一个整数 t' 代表 jl 死亡时的秒数。若 jl 活过了 t 秒，在一行内输出survive，并输出一个整数 a 代表 jl 对幻翼造成的总伤害数值。

对第一个测试，在第 1 秒，jl 与幻翼战斗；在第 4 秒， jl 与幻翼战斗；在第 6 秒， jl 与幻翼战斗。前两次战斗造成 7 点伤害，但最后一次战斗时幻翼只有 6 点生命值，所以只造成了 6 点伤害。所以总伤害为 20 。

对第二个测试，在第 1 秒， jl 与第一只幻翼战斗；在第 2 秒， jl 与第二只幻翼战斗；在第 4 秒， jl 与第三只幻翼战斗；在第 5 秒， jl 与第四只幻翼战斗；在第 6 秒，jl 同时与前三只幻翼战斗；在第 7 秒， jl 与第四只幻翼战斗，之后再无战斗。有 6 秒发生过战斗，jl 一共扣除 18 点血，一共攻击 8 次，且伤害均为 7，所以总伤害为 56。

对第三个测试，前 8 秒与第二个测试完全相同，在第 9 秒，jl 同时与四只幻翼战斗并死亡。

对第四个测试，前 63 秒幻翼与 jl 距离大于 64，幻翼不移动。从第 64 秒开始幻翼朝 jl 方向移动。在第 95 秒， jl 和幻翼坐标分别是 (31,0),(33,0)。自始至终他们未相遇，故总伤害为 0。