2021 天梯赛选拔 / 蓝桥杯热身赛
Problem I. U 型锁(30 分)
众所周知,U型锁是U型的,这种U型我们可以用函数 y=x^{2}+bx+c 来表示, b 和 c 都是实数。
现在墙上有许多个钉子,我们想通过钉子把U型锁钉在墙上。一个U型锁至少要两个钉子才能固定,即U型锁对应的函数至少要穿过两个钉子对应的点坐标。
此外,我们为了让U型锁钉得更好看,U型锁的内部,即 y \gt x^{2}+bx+c 这片区域中不允许有任何钉子。请问有多少种U型锁的固定方法呢?
两个U型锁固定方法不同当且仅当对应函数的 b 和 c 至少有一个不同。
输入
第一行输入 n ,代表钉子的个数, 1 \leq n \leq 1000 。
接下来有 n 行,每行有两个整数,分别代表这个钉子的 x 坐标和 y 坐标,其绝对值不超过 10^{6} ,钉子之间的坐标互不重合。
输出
输出一个整数,表示有多少种不同的U型锁固定方法。
样例
| 标准输入 复制文本 |
3 -1 0 0 2 1 0 |
| 标准输出 复制文本 |
2 |
| 标准输入 复制文本 |
5 1 0 1 -1 0 -1 -1 0 -1 -1 |
| 标准输出 复制文本 |
1 |
提示
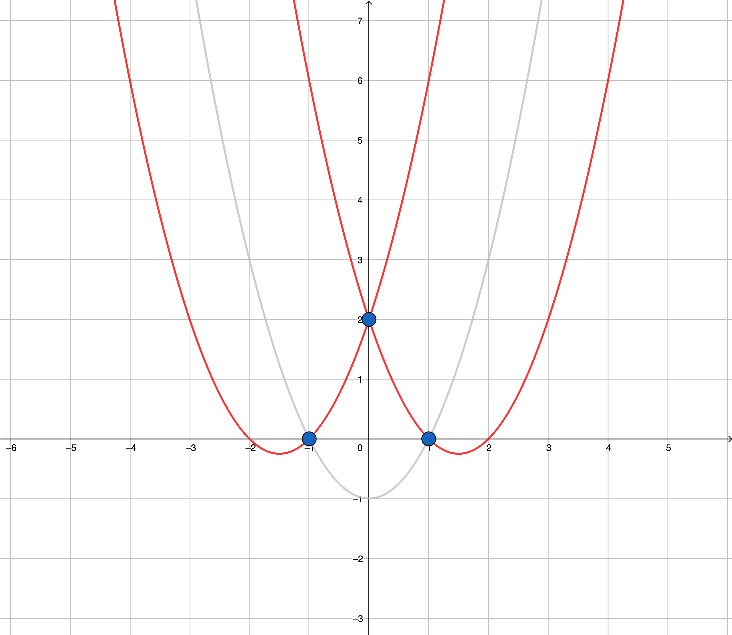
样例1中两个符合条件的U型锁的示意图。
对于 10 分的数据,n \leq 10 。
对于 20 分的数据,n \leq 100 。
对于 30 分的数据,n \leq 1000 。
登录以提交代码。