2022 软件学院 ACM 集训队筛选赛
Problem G. Living in Peace with Errors
Hefeng wakes up and tolds everything to her friends. With their efforts, Hefeng finally persuades Yunyan to choose a peace way. They keep constructing the Blue Planet, making it even more prosperous and developed.
Later, Tianjiang comes back and notices the note left by Hefeng. With curiosity, he goes to the Blue Planet. He is greatly thrilled at the miracles they made. It's a world combines technology with magic perfectly which is better than any other worlds created by Tianjiang. Everything here is living in peace. So Tianjiang decides not to remove the Abyss and appoints Yunyan as the administrator of the Blue Planet, hoping to observe greater achievements they could make.
Construction completed, new construction options... Having a brand new life, Yunyan is now burying himself constructing the Blue Planet energetically.
Yunyan can construct some buildings on the Blue Planet, and each building can have some(or none) relationships with other buildings. Each building has a positive integer value p , and if a building has d relationships with other buildings, then it has p^d contributions. The total contributions t is the sum of contributions of all the buildings.
Given total contributions t, you can assign value p for each building, and construct n buildings with at most 5800 relationships in total. Please construct a scheme to make the total contributions equal to t and output this scheme. If none of schemes is available, please output -1.
输入
A single line with an integer t(1\le t\le10^{9}) .
输出
If there exists scheme to get total contributions of t :
Output an integer n(1\le n\le580) in the first line denoting the number of buildings you construct.
Output n integer in the second line, the i-th integer p_i(2\le p_i\le58) denotes the important value of the i-th building.
Then output n lines, each line includes n integers. The i-th line's j-th integer is c_{ij} . If c_{ij}=1 , it denotes that the i-th building has relationship with the j-th building. If c_{ij}=0 , they have no relationship. You should guarantee that \forall1\le i,j\le n, c_{ij}=c_{ji} , c_{ii}=0 and \sum_{i=1}^n\sum_{j=1}^ic_{ij}\le 5800, 0\le c_{ij}\le 1.
If multiple schemes are available, output any of them.
If there is not exist any schemes to get total contributions of t , output -1 in an single line.
样例
| 标准输入 复制文本 |
580 |
| 标准输出 复制文本 |
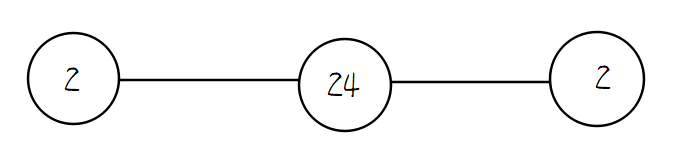
3 2 24 2 0 1 0 1 0 1 0 1 0 |
| 标准输入 复制文本 |
1437 |
| 标准输出 复制文本 |
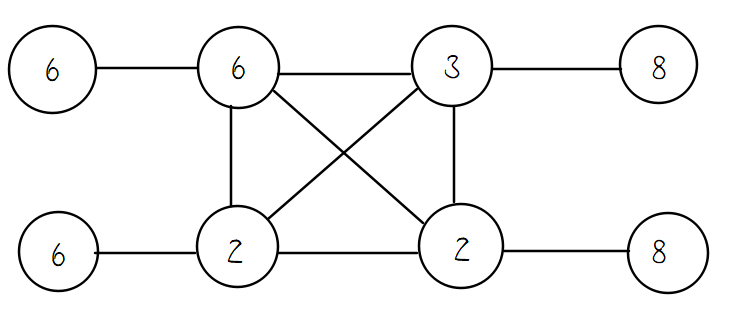
8 6 6 3 8 6 2 2 8 0 1 0 0 0 0 0 0 1 0 1 0 0 1 1 0 0 1 0 1 0 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 1 0 1 0 1 0 0 1 1 0 0 1 0 1 0 0 0 0 0 0 1 0 |
提示
In the first example, one possible scheme is like this, t=2^1+24^2+2^1=580:
In the second example, one possible scheme is like this,
t=6^1+6^4+3^4+8^1+6^1+2^4+2^4+8^1=1437 :